4. Héritage

4.1. Une bibliothèque ©

Pour la gestion d’une bibliothèque on nous demande d’écrire une application traitant des documents de nature diverse : des livres, des revues, des dictionnaires, etc. Les livres, à leur tour, peuvent être des romans ou des manuels.

Tous les documents ont un numéro d’enregistrement (un entier) et un titre (une chaîne de caractères). Les livres ont, en plus, un auteur (une chaîne) et un nombre de pages (un entier). Les romans ont éventuellement un prix littéraire (un entier conventionnel, parmi : GONCOURT, MEDICIS, INTERALLIE, etc.), tandis que les manuels ont un niveau scolaire (un entier). Les revues ont un mois et une année (des entiers) et les dictionnaires ont une langue (une chaîne de caractères convenue, comme "anglais", "allemand", "espagnol", etc.).

Tous les objets en question ici (livres, revues, dictionnaires, romans, etc.) doivent pouvoir être manipulés en tant que documents.

A. Définissez les classes Document, Livre, Roman, Manuel, Revue et Dictionnaire, entre lesquelles existeront les liens d’héritage que la description précédente mentionne.

Dans chacune de ces classes définissez

Écrivez une classe exécutable TestDocuments qui crée et affiche plusieurs documents de types différentes.

B. Une bibliothèque sera réalisée, au choix, soit par un tableau de documents, soit par un objet Vector dont les éléments sont des documents. Définissez une classe Bibliotheque, avec une telle structure de données pour variable d’instance privée et les méthodes :

C. Définissez, avec un effort minimal, une classe Livrotheque dont les instances ont les mêmes fonctionnalités que les bibliothèques mais sont entièrement constituées de livres. Comment optimiser dans la classe Livrotheque la méthode afficherAuteurs ?

4.2 Disques et anneaux

A. Définissez une classe Disque comportant trois variables d’instance privées de type double : x, y, les coordonnées du centre du disque et r, le rayon de celui-ci. Munissez cette classe des méthodes publiques suivantes :

• public Disque(double x, double y, double r) – constructeur standard
• public String toString() – comme d’habitude
• public boolean equals(Object obj) – comme d’habitude
• public void translation(double a, double b) – translation du disque (a et b sont les coordonnées du vecteur de translation)
• public double aire() – calcul de la surface du disque

Écrivez une méthode principale pour tester tout cela.

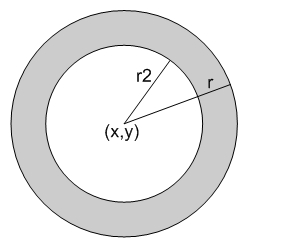
B. Définissez une classe Couronne, sous-classe de la précédente, en considérant qu’une couronne circulaire est un disque avec une variable d’instance supplémentaire, privée et de type double, r2, définissant le rayon du trou circulaire au centre du disque (voyez la figure ci-contre). Faites en sorte que les méthodes suivantes soient définies pour les couronnes :

• public Couronne(double x, double y, double r1, double r2) – constructeur standard
• public String toString() – comme d’habitude
• public boolean equals(Object obj) – comme d’habitude
• public void translation(double a, double b) – translation du disque (a et b sont les coordonnées du vecteur de translation)
• public double aire() – calcul de la surface du disque

4.3 Polygones ©

Pour faire cet exercice vous devez disposer d’une classe Point avec – au moins – deux membres d’instance privés x et y de type double, un constructeur public Point(double x, double y), des accesseurs public double getX() et public double getY() et l’habituelle transformation en chaîne de caractères public String toString(). La classe Point définie à la série précédente devrait faire l’affaire.

A. Définissez une classe Polygone comportant la variable d’instance :

et les méthodes :

B. Définissez une classe Triangle, sous-classe de Polygone, avec un constructeur

C. Définissez une classe Rectangle (sous-entendu, ayant des côtés parallèles aux axes), sous-classe de Polygone, munie d’un constructeur

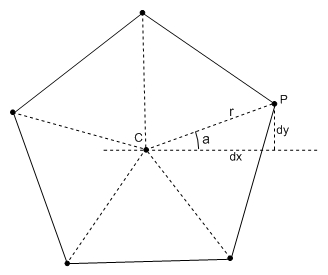
D. Définissez une classe PolygoneRegulier, sous-classe de Polygone, disposant d’un constructeur

E. Écrivez une classe TestPolygone avec une méthode main construisant et affichant des polygones de diverses sortes et permettant de vérifier que la méthode aire est correcte.

Voyez-vous pourquoi certains membres de la classe Polygone ont été déclarés protected au lieu de private ? Aurions-nous pu faire autrement ?

Indications, 1. Voici une manière de calculer l’aire S d’un polygone ayant les sommets (x₀, y₀), (x₁, y₁), ... (x_n-1, y_n-1) :

S = ½ | (x₀ – x₁) × (y₀ + y₁) + (x₁ – x₂) × (y₁ + y₂) + ... + (x_{n – 2} – x_{n – 1}) × (y_{n – 2} + y_{n – 1}) + (x_n – 1 – x₀) × (y_{n – 1} + y₀) |

Indications, 2. Un polynôme régulier peut être défini par son nombre n de sommets (n = 5 sur la figure), son centre C = (x_c, y_c) et un de ses sommets, P = (x_p, y_p). Pour déterminer les autres sommets, posons dx = x_p – x_c, dy = y_p – y_c, r = sqrt(dx² + dy²) et a = atan2(dy, dx). Les n sommets du polygone sont alors les points (x_i, y_i) définis par :

x_i = x_c + r × cos (a + i × 2 × pi / n)   ;   y_i = y_c + r × sin (a + i × 2 × pi / n)

4.4 Héritage ou composition ? ©

Prérequis. Si vous ne l’avez pas encore fait, jetez un œil sur la documentation de la classe java.util.Vector. Un vector V se comporte comme un tableau T, c’est-à-dire qu’il offre l’accès indexé optimisé (on dit « en temps constant ») à ses éléments, sauf qu’au lieu de « x = T[i] » il faut écrire « x = V.get(i) » et au lieu de « T[i] = x » il faut écrire « V.set(i,x) ». Cependant, un vector a un avantage considérable sur un tableau : il s’occupe de l’allocation de son espace mémoire, l’augmentant lorsque c’est nécessaire, sans que le programmeur ait à s’en soucier.

Exercice. Un journal est une collection d’événements. Un événement est fait de deux champs : une date et un texte. Un journal doit posséder les opérations suivantes :

• unJournal.ajouter(unTexte) – ajout au journal d’un événement composé de la date courante (que cette méthode obtient automatiquement) et du texte indiqué
• unJournal.toString() – renvoie une chaîne de caractères contenant tous les événements du journal
• unJournal.toString(uneChaine) – renvoie une chaîne de caractères contenant tous les événements dont le texte contient la chaîne indiquée

N.B. Pour les dates, revoyez si nécessaire l’exercice 3 de la série 1.

A. Écrivez une classe Evenement et une classe Journal. La classe Evenement, interne à Journal, sera aussi simple que possible (les deux champs indiqués, un constructeur élémentaire et la méthode toString habituelle).

Dans cette question, la classe Journal doit être une sous-classe de java.util.Vector.

B. Écrivez une classe TestJournal avec une méthode main simple qui lit et exécute des commandes comme  :

C. Réécrivez la classe Journal mais, au lieu d’en faire une sous-classe de Vector mettez-y un membre de type Vector. La classe TestJournal doit fonctionner sans changement.

D. Etre ou avoir ? Dans la question A vous avez lié les classes Vector et Journal par un lien d’héritage : un objet Journal « est » un objet Vector ; dans la question C vous les avez liés par un lien de composition : un objet Journal « a » un objet Vector. D’après vous, quels sont les mérites de l’une et l’autre manière de faire?

Dans quel cas contrôlez-vous mieux le comportement d’un objet Journal ? Supposez qu’on vous demande d’interdire les suppressions d’événements du journal ; est-il facile d’obtenir cela dans la solution A ?

Voyez-vous dans quelle situation l’héritage peut-il devenir préférable, voire nécessaire ?

4.5 Abstraction, classes abstraites, interfaces ©

Dans cet exercice on vous demande de définir un ensemble de classes pour représenter des fonctions d’une variable formées avec des constantes, des occurrences de la variable x, les quatre opérations arithmétiques +, –, ×, / et des appels de quelques fonctions convenues comme sin, cos exp, log, etc. Par exemple :

f(x) = 12 × x + sin(3 × x – 5)

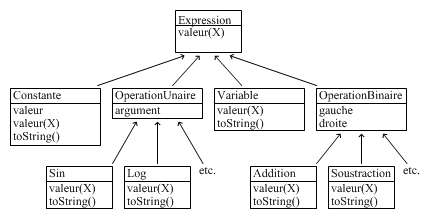
Dans un programme, une expression comme celle-là peut être efficacement représentée par une structure arborescente, organisée comme le montre la figure ci-contre, faite de feuilles (les constantes et les variables), de nœuds à deux « descendants » (les opérateurs binaires) et de nœuds à un descendant (les fonctions d’une variable).

Les classes qu’il faut définir sont destinées à représenter les nœuds d’un tel arbre. Il y en a donc de plusieurs sortes :

• un nœud représentant une constante porte un nombre, la valeur de la constante,
• un nœud représentant une occurrence de la variable x ne porte aucune autre information,
• un nœud représentant une addition, une soustraction, une multiplication ou une division porte deux informations : les expressions qui sont ses opérandes,
• un nœud représentant l’appel d’une fonction porte comme information l’expressions qui est son argument.

Définissez les classes suivantes (la marge traduit la relation implements ou extends)  :

Expression – interface représentant ce qu’ont en commun toutes les expressions arithmétiques (c’est-à-dire toutes les sortes de nœuds de notre structure arborescente) : elle se compose d’une seule méthode :     

public double valeur(double x);   

qui renvoie la valeur de l’expression pour la valeur de x donnée. Bien entendu, toutes les classes concrètes de cette hiérarchie devront fournir une définition de la méthode valeur. Elles fourniront aussi une reéfinition intéressante de la méthode String toString().

Constante – classe concrète dont chaque instance représente une occurrence d’une constante. Cette classe a un membre : la valeur de la constante.

Variable – classe concrète dont chaque instance représente une occurrence de la variable x. Cette classe n’a besoin d’aucun membre.

OperationBinaire – classe abstraite rassemblant ce qu’ont en commun tous les opérateurs à deux opérandes. Elle a donc deux membres d’instance, de type Expression, représentant les deux opérandes, et le constructeur qui va avec.

Addition, Soustraction, Multiplication, Division – classes concrètes pour représenter les opérations binaires. C’est ici qu’on trouve une définition pertinente de la méthode valeur promise dans l’interface Expression.

OperationUnaire – classe abstraite rassemblant ce qu’ont en commun tous les opérateurs à un opérande. Elle doit avoir un membre d’instance, de type Expression, représentant l’opérande en question.

Sin, Cos, Log, Exp, etc. – classes concrètes pour représenter les fonctions standard. Ici on doit trouver une définition pertinente de la méthode valeur promise dans l’interface Expression.

On ne vous demande pas de résoudre le problème (difficile) de la « lecture » d’un tel arbre, c’est-à-dire de sa construction à partir d’un texte, par exemple lu à la console. En revanche, vous devez montrer que votre structure est bien adaptée au calcul de la valeur de l’expression pour une valeur donnée de la variable x. Pour cela, on exécutera un programme d’essai comme celui-ci :

    ...
    public static void main(String[] args) {

            /* codage de la fonction f(x) = 2 * sin(x) + 3 * cos(x) */
        Expression f = new Addition(
                new Multiplication(
                        new Constante(2), new Sin(new Variable())), 
                new Multiplication(
                        new Constante(3), new Cos(new Variable())));
        
            /* calcul de la valeur de f(x) pour quelques valeurs de x */
        double[] tab = { 0, 0.5, 1, 1.5, 2, 2.5 };

        for (int i = 0; i < tab.length; i++) {
            double x = tab[i];
            System.out.println("f(" + x + ") = " + f.valeur(x));
        }
    }
    ...

L’exécution de ce programme produit l’affichage de :

f(0.0) = 3.0
f(0.5) = 3.5915987628795243
f(1.0) = 3.3038488872202123
f(1.5) = 2.2072015782112175
f(2.0) = 0.5701543440099361
f(2.5) = -1.2064865584328883

4.6 Interfaces et objets fonctionnels ©

On s’attaque ici au problème suivant : comment obtenir en Java qu’une fonction puisse avoir pour argument une autre fonction ?

Par exemple, la méthode dite dichotomie est une technique de résolution approchée d’équations de la forme « f(x) = 0 ». Sous réserve que f soit une fonction continue (c’est-à-dire « sans sauts ») et qu’on connaisse deux valeurs a et b telles que les signes de f(a) et de f(b) soient opposés, alors cette méthode trouve rapidement une valeur z, comprise entre a et b, qui n’est pas plus éloignée que epsilon d’une solution de l’équation, où epsilon est une précision arbitraire fixée à l’avance. Dit autrement : la méthode trouve z tel que f(z) = 0 avec une erreur inférieure à epsilon.

L’algorithme est bien connu ; en voici une programmation (méthode zero) accompagnée d’un essai consistant à résoudre x² – 4 = 0 (c’est-à-dire à trouver la racine carrée de 4) avec une précision de 10^-12 (à l’exécution, ce programme affiche 1.9999999999995453) :

public class TestDichotomie {
    
    /* essai de la méthode zero */
    public static void main(String[] args) {
        double y = zero(0, 4, 1e-12);
        System.out.println(y);
    }

    /* la fonction f(x) = x * x - 4 */
    static double f(double x) {
        return x * x - 4;
    }
    
    /* la méthode elle-même (on suppose que f(a) et f(b) sont de signes distincts) */
    static double zero(double a, double b, double epsilon) {

        /* si on n’a pas f(a) < 0 on échange a et b */
        if (f(a) > 0) {
            double w = a; a = b; b = w;
        }

        /* iterations jusqu’à avoir |a - b| <= epsilon */
        while (Math.abs(b - a) > epsilon) {
            double c = (a + b) / 2;
            if (f(c) < 0)
                a = c;
            else
                b = c;
        }
	    
        /* lorsque |a - b| <= epsilon, n'importe quelle valeur comprise entre a et b convient */
        return (a + b) / 2;
    }
}  

Écrite comme cela, la méthode zero fonctionne mais elle est peu réutilisable, car elle emploie une fonction f qui ne figure pas parmi ses arguments. Pour trouver un zéro d’une autre fonction il faut changer le corps de f et compiler de nouveau ce programme ! Plus grave, puisque f est figé, on ne peut pas dans le même programme utiliser zero sur des fonctions différentes.

On va donc faire en sorte que la fonction f figure parmi les arguments de zero :

static double zero(Fonction f, double a, double b, double epsilon)

où Fonction représente le type « fonction qu’il faut appeler avec un argument double et qui renvoie un résultat double ». On introduit donc l’interface :

public interface Fonction {
    double appel(double x);
}

Exercice. Réécrivez la méthode zero en prenant en compte qu’elle a désormais un objet Fonction comme premier argument, ensuite écrivez une fonction main qui résout l’équation cos(x) = x (c'est-à-dire cos(x) – x = 0) avec une erreur inférieure à 10^-10.

Écrivez l’essai (la méthode main) de deux manières, sans utiliser puis en utilisant les classes anonymes.

4.7 Héritage multiple et Java ©

En Java l’héritage est simple : chaque classe a une et une seule super-classe (sauf Object, qui n’en a pas). Mais alors, comment faire lorsque les objets d’un certain type doivent être considérés comme appartenant à deux hiérarchies d’héritage, ou plus ?

Question préalable : pourquoi serait-on obligé de déclarer une classe C comme héritant de deux autres classes A et B ? Si on veut que les membres de A et ceux de B soient membres de C, ne suffit-il pas de mettre dans C une variable de type A et une variable de type B ?

Réponse. Il est nécessaire que C soit sous-classe de A [resp. B] si on veut pouvoir mettre un objet C à un endroit où est attendu un objet A [resp. B] est attendu. Par exemple, si on dispose d’une méthode ayant un argument formel de type A, une deuxième méthode avec un argument formel de type B et qu'on a besoin de les appeler l'une et l'autre avec un objet de type C, alors il faut que la classe C soit sous-classe de A et de B.

Exemple (à vrai dire, un peu tiré par les cheveux... mais c’est un bon exemple) :

Nous supposerons que Personnel, Enseignant et Chercheur sont trois classes concrètes (c'est-à-dire non abstraites), précédemment définies, parfaitement opérationnelles. Pour le test, nous supposerons que des méthodes sont disponibles par ailleurs, qui prennent pour argument des instances de chacune de ces classes :

L’exercice est le suivant : définir un type PersonnelEnseignantChercheur destiné à représenter des personnels de l’éducation nationale qui sont en même temps des enseignants et des chercheurs.

Bien entendu, il faut faire cela avec un minimum d’effort, un maximum de fiabilité et selon une méthodologie qui puisse être employée chaque fois que le même genre de problème se posera.